Back in November, I found myself curious about spontaneous synchronisation in coupled oscillating systems. A particularly striking example is the synchronisation of metronomes.

I wanted to see if I could write a very simple program that replicates this effect, and took very heavy inspiration from the excellent firefly simulation built by Nicky Case.

The Synchronisation of Firefly Flashes

Bioluminescent synchronisation is a phenomenon that has been observed for some time, a famous account is that of the German physician and explorer, Engelbert Kaempfer, who wrote of his 1680 voyage near Bangkok

For a more contemporary account, we shift our attention to the work of the John and Elisabeth Buck. In 1968, the Bucks published a paper describing their findings on the Mechanism of Rhythmic Synchronous Flashing of Fireflies from their visit to Thailand (Buck & Buck, 1968). It was established that at an ambient temperature of 28℃ fireflies located in trees flash synchronously approximately once every 560ms, with a maximum range of coincidence being around 20ms (Buck & Buck, 1968). As for the title, it was postulated that …the initial entrainment could involve progressive phase-shifting, operating either over the whole range of temporal separation or after the rhythms have drifted to within a certain degree of approximation. In other words, it was speculated that upon seeing its neighbour flash, a nearby firefly may flash (thus resetting its rhythm) either regardless of its current state or only if it is already close to flashing. Over time, this mechanism would lead to a grouping effect, where clusters of neighbouring fireflies flash simultaneously, until eventually, these clusters merge and the entire collection flashes in synchrony.

The brilliant insight of Nicky Case is that we can translate this to a very simple set of rules, on which I also base my program,

1. Each firefly has an internal clock, and, upon one full revolution, the firefly will flash
2. If, within some radius around the firefly, a neighbouring firefly flashes, the internal clock will progress by one tick...

That’s it! The rest just comes down to how we define the movement of the fireflies, their radius of interaction, and the frequency of their flashes. In my program, their movement is dictated by a uniform distribution, and in order to avoid grouping at the edges of their container, I impose a periodic boundary. Furthermore, I make the light of each flash linger on screen for two time steps, to help us better see where clustering is taking effect.

We can now observe the synchronisation of fireflies:

Here we are simulating 100 fireflies, and the luminosity at a single point in time is defined as the number of fireflies that are lit up. We see that initially the luminosity is random, as most fireflies are out-of-sync with one-another, however after approximately 100 steps we start to see the effects of clustering, with three very well defined peaks, if you look closely, you will see that each peak actually represents two large clusters that are one step out-of-sync with each other (this is due to my choice to allow the light to linger on screen). The fact that these peaks are staggered suggests the existence of a handful of clusters that are almost in-sync with one-another.

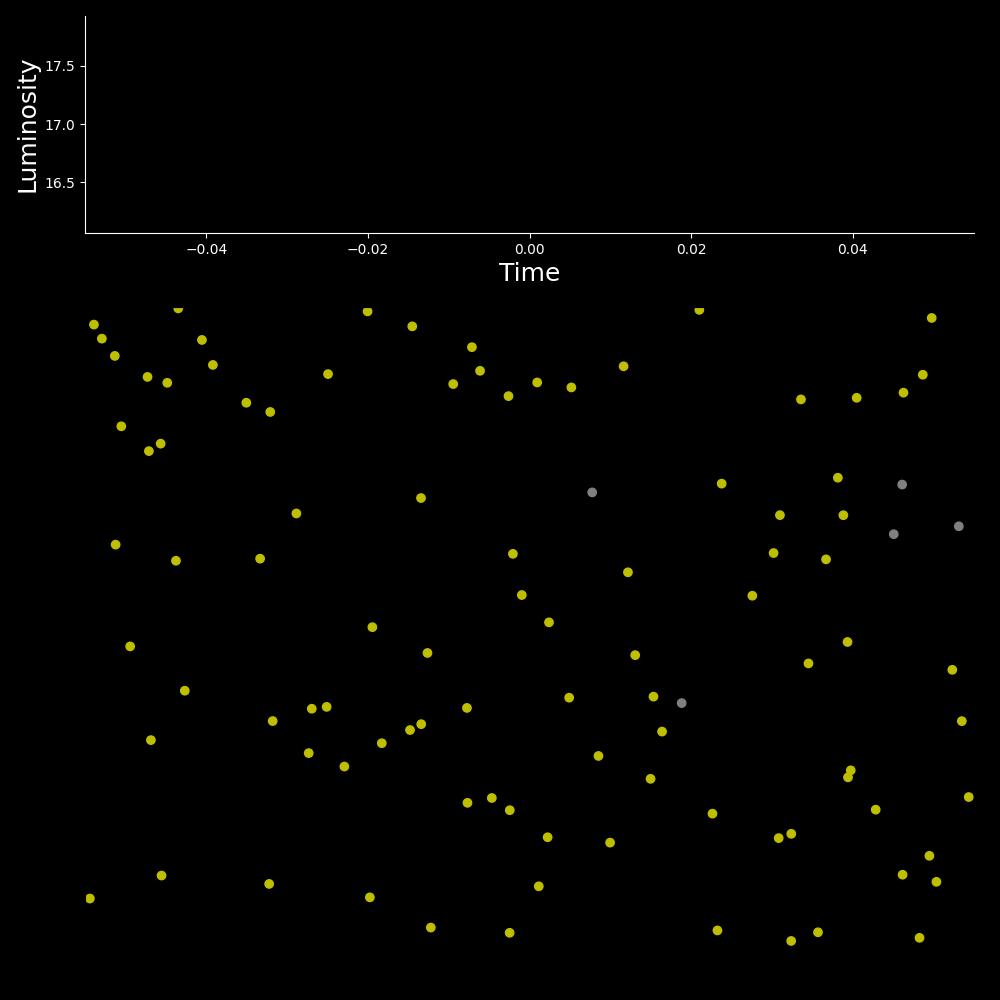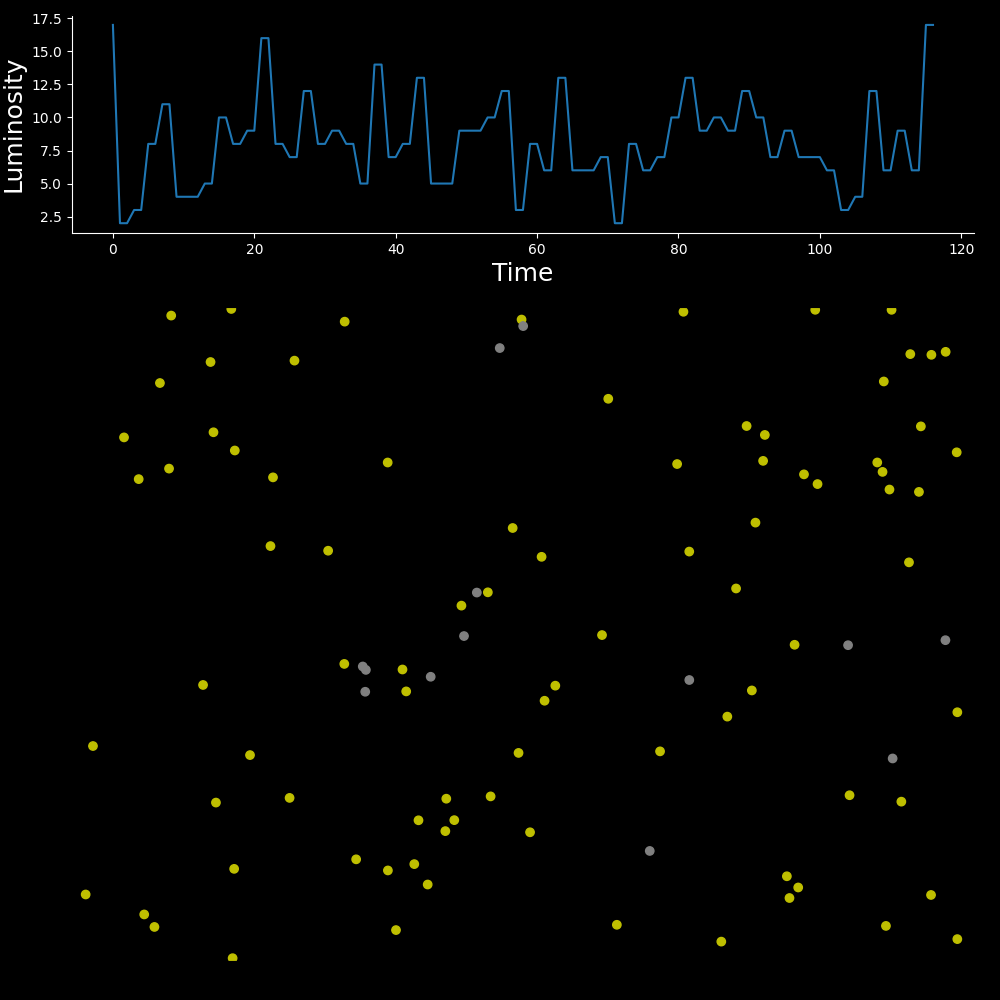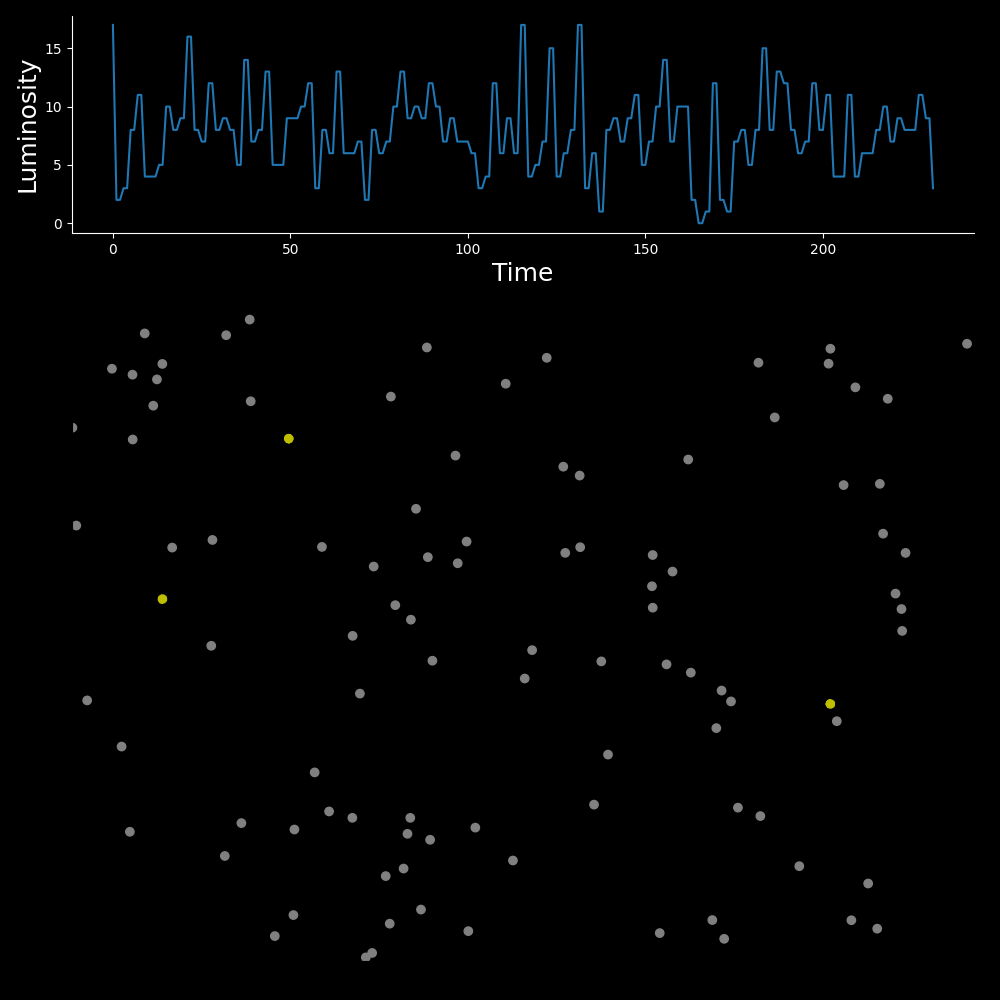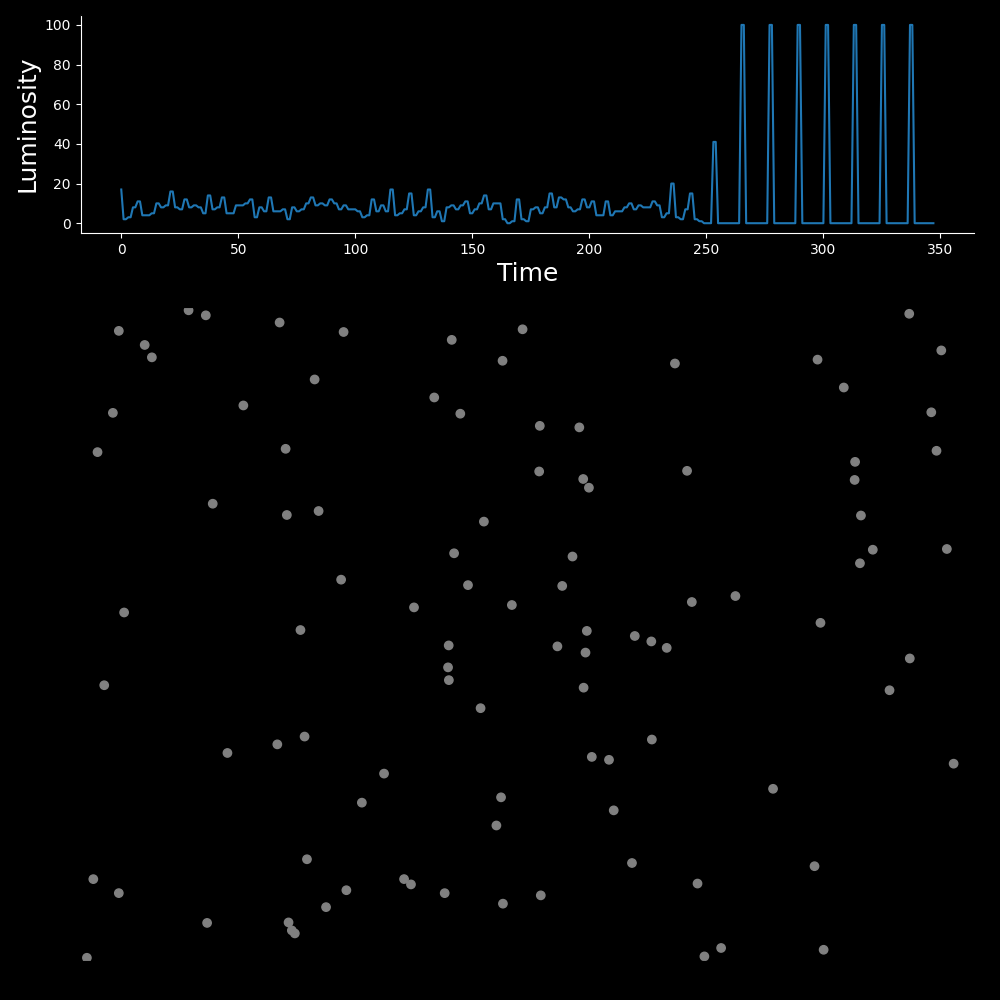
After approximately 230 steps, we begin to see the merging of these clusters, with a decrease in staggering and a rapid increase in amplitude at around 250 steps. At this point, the synchronisation of the whole group is locked in, because the two remaining clusters in the previous step have merged into one super cluster. Indeed, after this, we observe a dramatic increase in the luminosity to the number of fireflies, which remains periodic. It would appear that we have confirmed that the hypothesis of the Bucks is viable.

For more information on the Bucks, their lives, and their work, I recommend (Case & Hanson, 2004). Thank you for reading, I hope you found this interesting!

References

[1] Kaempfer, Engelbert. The history of Japan: together with a description of the kingdom of Siam, 1690-92. Vol. 3. J. MacLehose and sons, 1906.

[2] Buck, John, and Elisabeth Buck. “Mechanism of Rhythmic Synchronous Flashing of Fireflies: Fireflies of Southeast Asia may use anticipatory time-measuring in synchronizing their flashing.” Science 159.3821 (1968): 1319-1327.

[3] Case, James F., and Frank E. Hanson. “The luminous world of John and Elisabeth Buck.” Integrative and Comparative Biology 44.3 (2004): 197-202.